翻譯：工業(yè)藥劑發(fā)燒友

校對(duì)：華溶-代希林

一、摘要
本文提出了一種分析和比較溶出曲線（DP）的新方法，并通過案例研究加以說明。這個(gè)有用的策略是通過使用溶出曲線中所有的數(shù)據(jù)來建立兩種統(tǒng)計(jì)：曲線水平和曲線形狀。曲線水平與曲線下的面積相關(guān)，并反映患者對(duì)藥物的“暴露”程度。形狀與藥物溶出隨時(shí)間的速率有關(guān)。這些特征能夠客觀真實(shí)的解釋實(shí)驗(yàn)中研究的因素。該方法易于使用，只需要直線回歸和設(shè)計(jì)實(shí)驗(yàn)分析程序。當(dāng)所提出的模型不能充分描述數(shù)據(jù)時(shí)，建議采用主成分分析（MPCA）作為替代方法。

二.溶出曲線行為
溶出速率是片劑的關(guān)鍵質(zhì)量屬性。片劑溶出通常通過檢查DP的形式來研究，DP是片劑在不同時(shí)間點(diǎn)溶出的百分比。圖1顯示了五個(gè)這樣的DP：Shah等人的研究中包括1批參比制劑和4批仿制藥。圖1顯示了DP的典型類型。一些批次表現(xiàn)了在開始時(shí)的低溶出水平（例如，15分鐘時(shí)為25%-40%），而另一些開始15分鐘時(shí)約為75%。結(jié)果是具有各種溶出情況的DP集合。

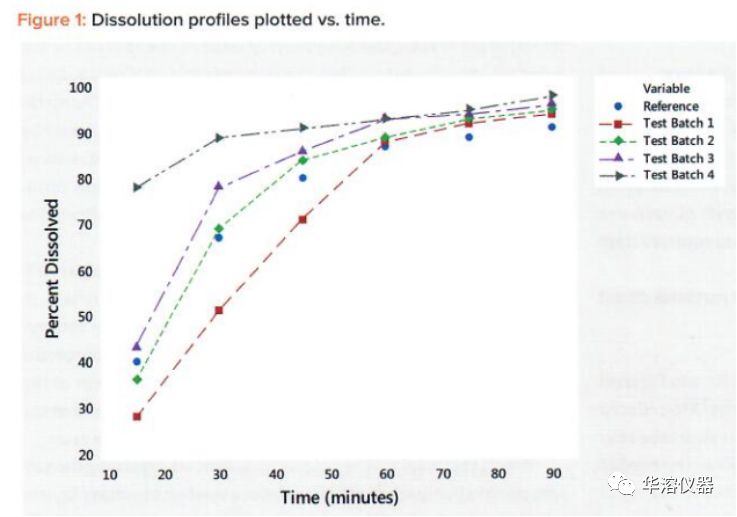通常進(jìn)行實(shí)驗(yàn)以研究各種因素對(duì)DP的影響。溶解分析中的復(fù)雜問題應(yīng)是：一個(gè)涉及多個(gè)數(shù)據(jù)點(diǎn)的響應(yīng)曲線，而不是一個(gè)響應(yīng)值。本文介紹了一種新的方法，該方法將曲線簡(jiǎn)化為兩個(gè)統(tǒng)計(jì)數(shù)據(jù)：曲線水平和曲線形狀。在圖1中，批次4曲線具有較高的平均值（水平）和較低的斜率（形狀）。批次1具有低平均值（水平）和高斜率（形狀）。其他DP（參比、批次2和批次3）位于測(cè)試批次1和4的DP之間，非常相似。這些觀察結(jié)果得到了表3所示的曲線平均值和斜率統(tǒng)計(jì)數(shù)據(jù)的支持，這將在本文后面介紹。
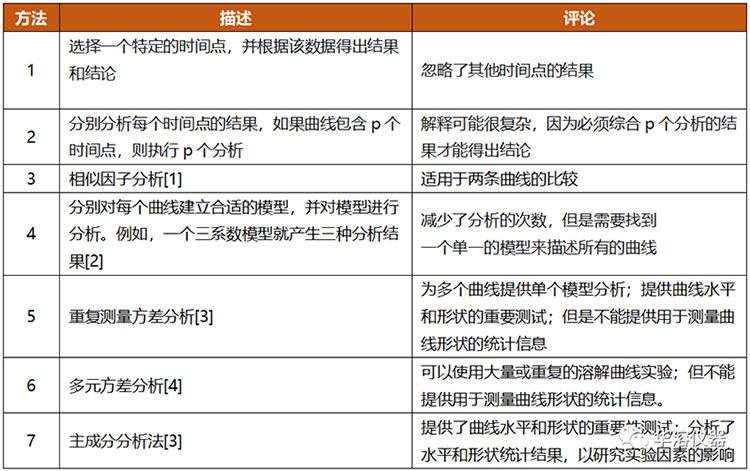
目前已經(jīng)有多種方法來分析DPs（見表1）。在回顧了可用的方法之后，描述所建立的新方法，并展示了新方法如何克服現(xiàn)有方法的局限性。

三、分析溶出實(shí)驗(yàn)的有效方法
已有幾種單變量和多變量方法來研究實(shí)驗(yàn)因素對(duì)DP的影響。表1總結(jié)了七種這樣的方法。在特定的情況下，每種方法都很有用。這些方法具有以下一般限制：方法1和方法2沒有利用DP中的所有信息。方法4要求各個(gè)模型適合各個(gè)DP。通常很難找到描述所有DP的單個(gè)模型。方法5、6和7需要使用復(fù)雜的統(tǒng)計(jì)程序，如重復(fù)測(cè)量方差分析（ANOVA）、主成分分析和多變量ANOVA方法。除方法7（MPCA）外，這些方法不直接處理DP水平和形狀。
需要提供與DP水平和形狀相關(guān)的統(tǒng)計(jì)信息的方法。在此過程中，DP上的點(diǎn)數(shù)縮小到這兩個(gè)統(tǒng)計(jì)值中。這個(gè)分析方法，應(yīng)易于理解、結(jié)果的說明以及執(zhí)行所需的計(jì)算。目標(biāo)是找到一種適用于各種情況的策略。

例1：線性溶出曲線
如前所述，溶出實(shí)驗(yàn)分析中的復(fù)雜問題是：響應(yīng)是涉及多個(gè)數(shù)據(jù)點(diǎn)的曲線，而不是單個(gè)響應(yīng)點(diǎn)。文獻(xiàn)中提出的方法通過各種類型的單變量或多變量統(tǒng)計(jì)分析來降低這種復(fù)雜性。但是單變量方法通常忽略重要信息，而多變量方法使用和解釋起來很復(fù)雜。
這里提出的目標(biāo)是找到一個(gè)基于時(shí)間的關(guān)系，當(dāng)繪制DP與時(shí)間關(guān)系時(shí)，將產(chǎn)生一條呈直線的形狀。時(shí)間關(guān)系是一個(gè)基于時(shí)間的量，它傳達(dá)了時(shí)間效應(yīng)的大小和性質(zhì)。其結(jié)果是將直線簡(jiǎn)化為兩個(gè)參數(shù)：斜率和截距。Rao和Mandel的工作表明，在許多情況下，總體的平均結(jié)果提供了這樣一個(gè)參數(shù)/關(guān)系。
Rao評(píng)論道：“這個(gè)成功之處在于：用少許的數(shù)據(jù)來代替對(duì)上升的溶出曲線的各種觀察結(jié)果，從而對(duì)各組之間進(jìn)行最有效的比較……
然而，時(shí)間可以通過函數(shù)r = G(t)進(jìn)行轉(zhuǎn)換，使得曲線上升速率相對(duì)于所選的時(shí)間是均勻的，這樣就可以用初始值和速率來充分表示。”換句話說，DP與時(shí)間的關(guān)系是一條直線。
DPs有兩個(gè)一般屬性:水平和形狀。理想的方法是用一個(gè)統(tǒng)計(jì)數(shù)據(jù)來衡量水平，用第二個(gè)統(tǒng)計(jì)數(shù)據(jù)來量化形狀。如果每個(gè)DP可以用如下形式的直線模型描述: Mandel顯示，對(duì)于雙向數(shù)據(jù)，“我們已經(jīng)看到了行線性模型是如何被理解為由一束直線組成的，每行一條直線，當(dāng)這些行與它們的公共列平均值相對(duì)應(yīng)時(shí)。”在Mandel的模型中，數(shù)據(jù)表的每一“行”都是一組實(shí)驗(yàn)條件產(chǎn)生的DP。
DPs有兩個(gè)一般屬性:水平和形狀。理想的方法是用一個(gè)統(tǒng)計(jì)數(shù)據(jù)來衡量水平，用第二個(gè)統(tǒng)計(jì)數(shù)據(jù)來量化形狀。如果每個(gè)DP可以用如下形式的直線模型描述:

A=曲線的平均值（曲線水平）

В=線性關(guān)系的斜率（曲線形狀）

APt=時(shí)間t的平均曲線值

APg=平均曲線的平均值
在該模型中，直線的斜率(B)和截距(A)概括了形狀的所有信息。在不喪失一般性的情況下，這個(gè)截距(A)是溶出的平均值。
截距（A）和斜率（B）具有重要的實(shí)際意義。平均值（A）是曲線的水平的統(tǒng)計(jì)值；通過測(cè)量曲線下的面積，反映藥物溶解開始后患者暴露于藥物的情況。斜率（B）反映了曲線形狀，并測(cè)量了溶解速率。例如，一個(gè)曲線DP的斜率B=1.20意味著相應(yīng)的曲線的溶出速率比平均曲線的溶出速率高20%。
溶解曲線線性化的方法
將使用圖1和表2所示的溶出數(shù)據(jù)說明DP線性化的方法。數(shù)據(jù)由一個(gè)參比制劑曲線數(shù)據(jù)和四個(gè)仿制藥數(shù)據(jù)組成。取6個(gè)時(shí)間點(diǎn)，包括：15、30、45、60、75和90分鐘。這些曲線數(shù)據(jù)的分析過程如圖2所示。

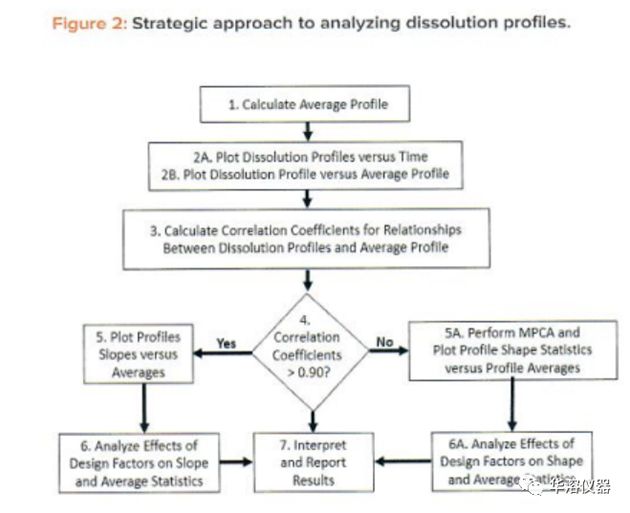
步驟1：
通過五個(gè)批次的每個(gè)時(shí)間點(diǎn)的溶出計(jì)算平均溶出度。例1的平均溶出度結(jié)果見表2的最后一列。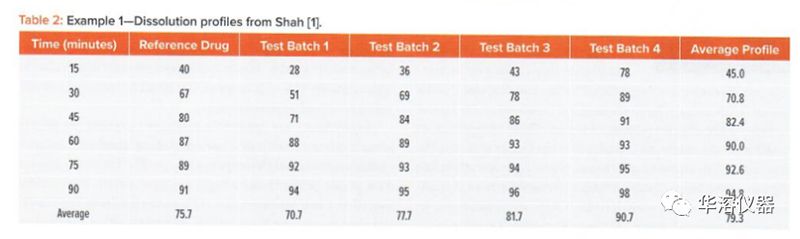
步驟2A：
每個(gè)批次的DP與時(shí)間的關(guān)系見圖1。在圖1中，DP顯示了一種凹形模式增加并穩(wěn)定在100%左右。顯示了不同的水平和形狀。例如，批次4的曲線從高起點(diǎn)開始并緩慢增加，而測(cè)試批次1的曲線從低起點(diǎn)開始并快速增加至100%。
步驟2B：
繪制每個(gè)批次的平均曲線，如圖3所示。在圖3中，我們看到當(dāng)繪制平均曲線時(shí)，所有曲線都顯示出強(qiáng)烈的線性關(guān)系。該圖進(jìn)一步顯示了曲線平均值（水平）和曲線斜率（形狀）匯總了曲線中的信息。因此，我們將曲線上的六個(gè)點(diǎn)歸納為兩個(gè)統(tǒng)計(jì)數(shù)據(jù)。

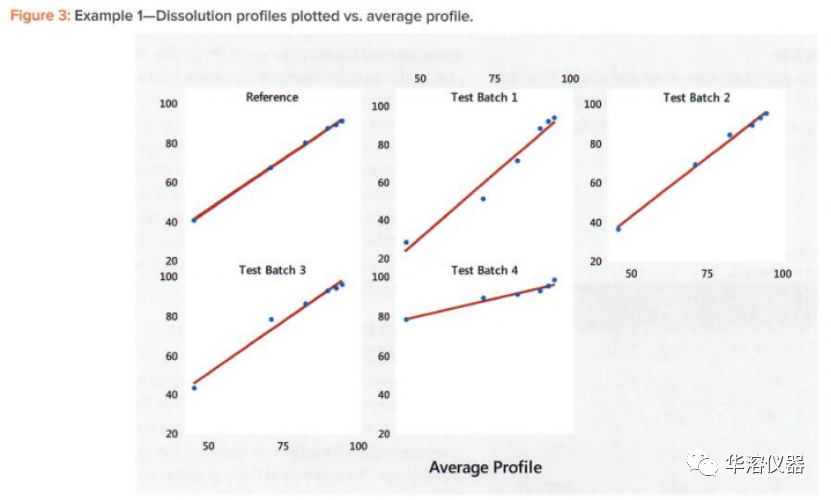
步驟3：
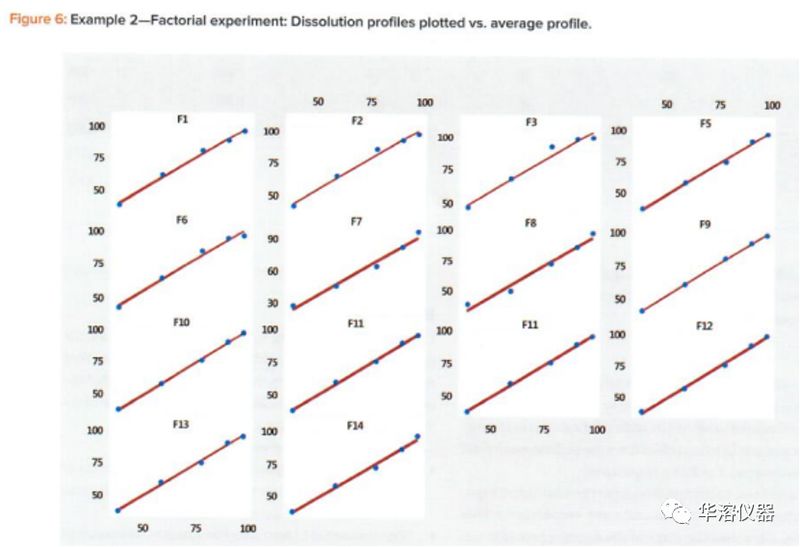
計(jì)算每個(gè)曲線的相關(guān)系數(shù)，以檢查線性關(guān)系擬合的充分性。
步驟4：
檢查步驟3中相關(guān)系數(shù)的大小。相關(guān)系數(shù)均大于0.983，證實(shí)了圖3中觀察到的強(qiáng)烈的線性關(guān)系。大于0.90的相關(guān)系數(shù)通常是強(qiáng)正相關(guān)，這表明可以使用每個(gè)線性的斜率與平均值的關(guān)系來評(píng)估實(shí)驗(yàn)結(jié)果。當(dāng)一個(gè)或多個(gè)相關(guān)系數(shù)小于0.90時(shí)，應(yīng)考慮使用Wang及其同事建議的MPCA。該方法可以在同一組實(shí)驗(yàn)結(jié)果中描述各種各樣的形狀。
步驟5：
計(jì)算每個(gè)線性關(guān)系的相關(guān)系數(shù)。表3中所示的五個(gè)曲線的A（水平）和B（斜率）統(tǒng)計(jì)結(jié)果表明，批次4和批次1表現(xiàn)了最高和最低平均值（水平）分別為90.7和70.7。批次4和批次1的斜率（形狀）值分別為0.361和1.376。這表明，由于平均斜率為1.0，第4批試驗(yàn)的斜率為平均剖面的36.1%。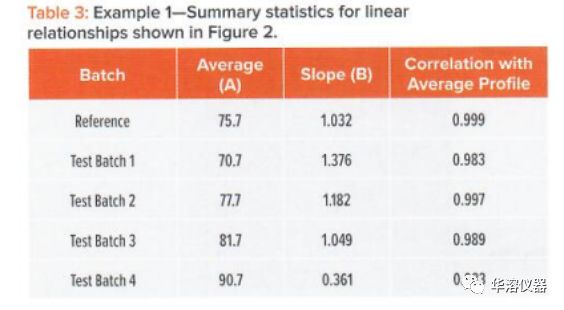
步驟5A：
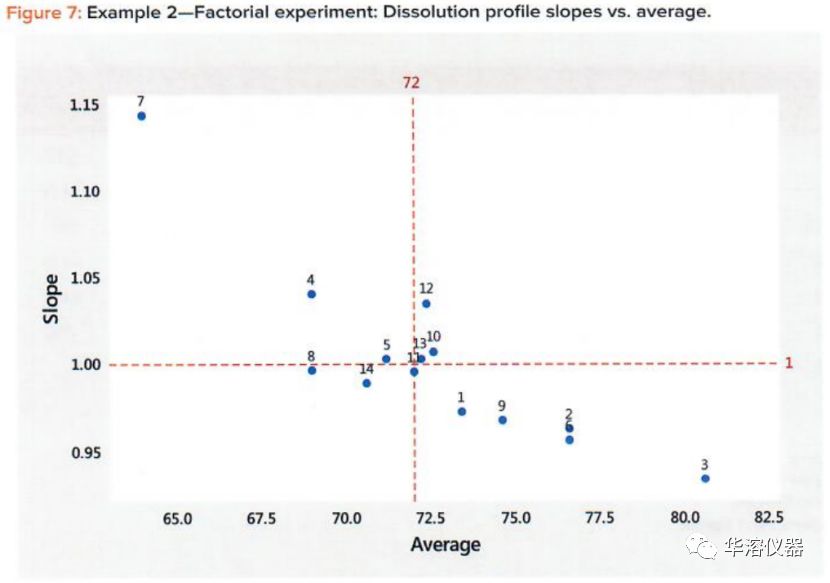
使用步驟5的結(jié)果，繪制直線的斜率（形狀）與平均溶出度（水平），以圖形方式查看它們之間的關(guān)系。為了方便觀察，可以繪制斜率=1和溶出度等分的平均值的虛線，如圖4所示。在圖4中，我們看到了幾個(gè)重要的模式：形狀和水平統(tǒng)計(jì)之間存在強(qiáng)烈的負(fù)相關(guān)，因?yàn)樾甭实驼f明在初始短時(shí)間15分鐘內(nèi)具有高溶出度。更重要的是，強(qiáng)相關(guān)性表明我們只需要分析溶出平均值（水平），因?yàn)橛捎谒胶托螤罱y(tǒng)計(jì)之間的相關(guān)性，形狀的分析將產(chǎn)生相同的結(jié)果。水平和形狀統(tǒng)計(jì)之間的強(qiáng)相關(guān)性對(duì)于DP來說并不罕見。在本例中，相關(guān)性為負(fù)。在曲線開始時(shí)處于低溶解水平的情況下，相關(guān)性將是正的。重要的考慮因素是相關(guān)性強(qiáng)度，而不是其方向。強(qiáng)相關(guān)性（正相關(guān)性或負(fù)相關(guān)性）表明可以通過分析其水平統(tǒng)計(jì)數(shù)據(jù)來比較配置文件。重要的考慮因素是相關(guān)性強(qiáng)度，而不是其方向。強(qiáng)相關(guān)性（正相關(guān)性或負(fù)相關(guān)性）均表明可以通過分析其溶出平均值（水平）來比較溶出情況。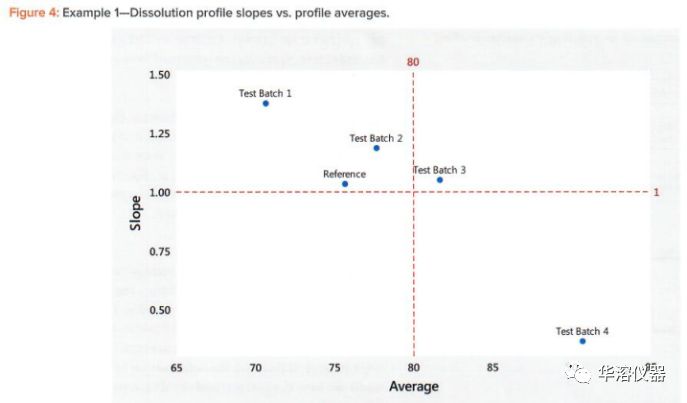
步驟6：
根據(jù)實(shí)驗(yàn)設(shè)計(jì)中的變化源分析水平和形狀。該步驟將在實(shí)施例2中討論的3×3析因?qū)嶒?yàn)的分析中說明。
步驟7：
描述和報(bào)告試驗(yàn)結(jié)果。
例2：采用3*3因子設(shè)計(jì)溶出實(shí)驗(yàn)
實(shí)施例2涉及使用3×3因子設(shè)計(jì)研究?jī)煞N成分對(duì)依非韋侖片溶出的影響的實(shí)驗(yàn)。該設(shè)計(jì)由9個(gè)試驗(yàn)點(diǎn)組成，其中14個(gè)處方的中有5個(gè)重復(fù)點(diǎn)（處方5、10-14）。表4顯示了生成的DP。表5中提供了構(gòu)成14種處方中每一種的成分。對(duì)于實(shí)施例2，前面和圖2中描述的分析步驟1-5產(chǎn)生了以下結(jié)果：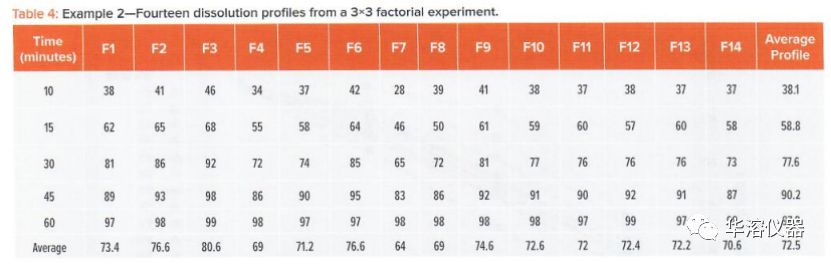
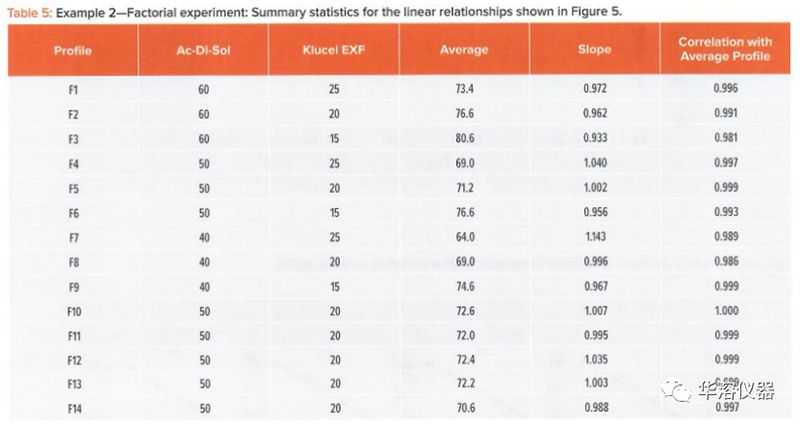
繪制溶出與時(shí)間的關(guān)系圖顯示了一系列典型的DP凹曲線（圖5）。繪制每個(gè)曲線與平均曲線表明，線性擬合良好（表4，圖6）。14個(gè)曲線圖的線性相關(guān)系數(shù)范圍為0.981至1.000（表5）。顯示出強(qiáng)烈的負(fù)相關(guān)（圖7），表明隨著溶出水平的增加，斜率減小。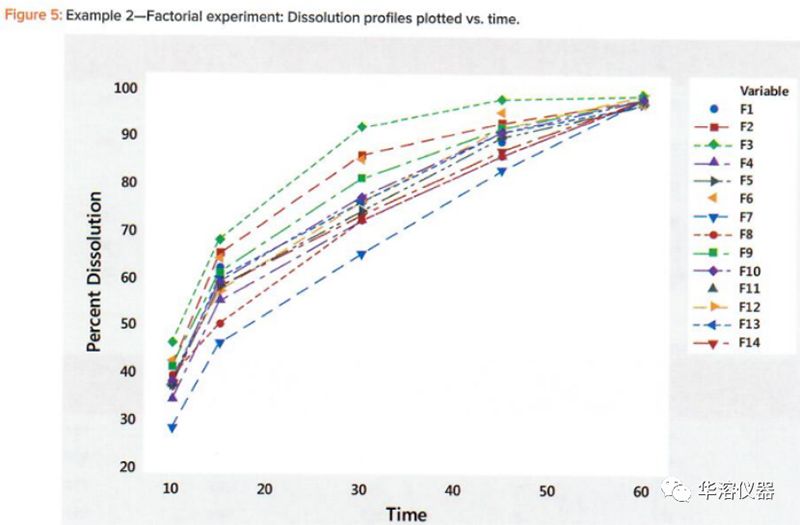
分析中的第6步是研究?jī)煞N成分（X1=Ac-Di-Sol和X2-Klucel EXF）對(duì)DP的平均值（水平）和斜率（形狀）的影響。分別針對(duì)平均值和斜率值開發(fā)了如下形式的模型：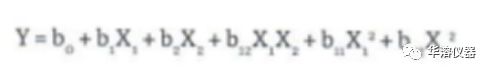

X1是Ac-Di-Sol的量、X2是Klucel EXF的量
以標(biāo)準(zhǔn)化形式擬合這些模型的結(jié)果如表6所示。結(jié)果表明，兩個(gè)變量都存在統(tǒng)計(jì)上顯著的線性和相互作用效應(yīng)。線性項(xiàng)占主導(dǎo)地位。二次項(xiàng)沒有統(tǒng)計(jì)學(xué)意義。這些模型很好地解釋了數(shù)據(jù)；平均值和斜率的調(diào)整后R值分別為97%和82%。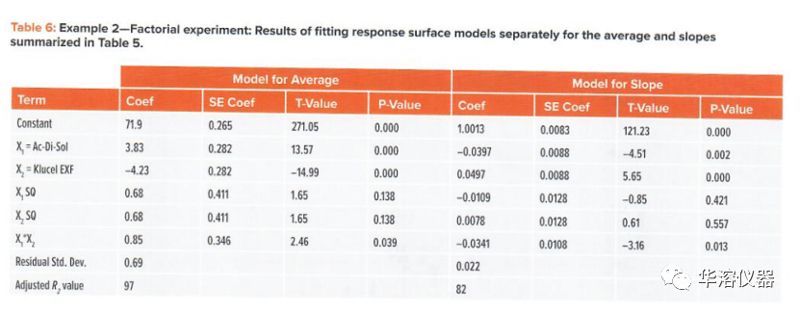

觀察這些影響的最佳方法是檢查圖8所示平均值和斜率的響應(yīng)面等高線圖。我們?cè)趫D6中看到的溶出平均值和斜率之間的負(fù)關(guān)系在圖8中很明顯，其中高平均值處于低X1-高X2，高斜率值處于高X1-低X2值。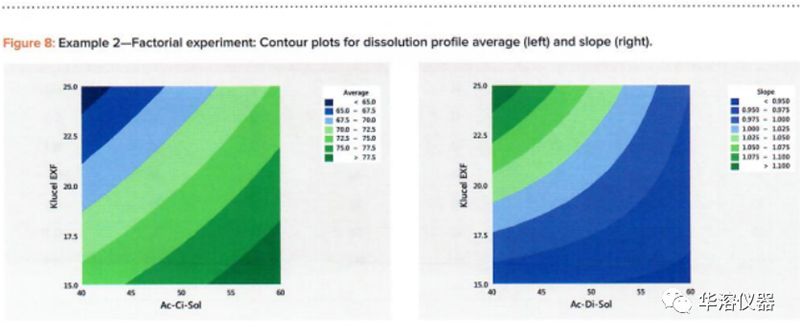
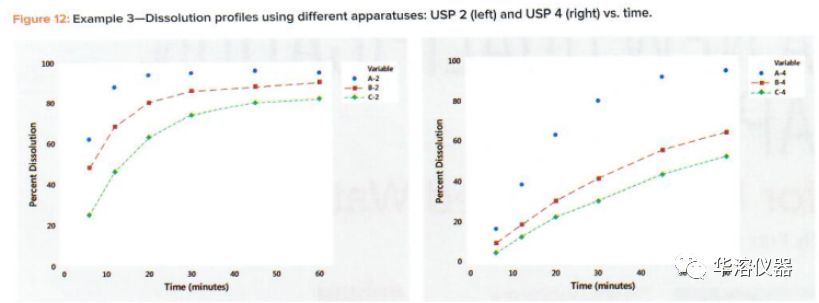
例3：使用不同的IISP設(shè)備比較溶解曲線
繪制DPs和平均溶出圖有時(shí)并不能同樣地適合所有的曲線。當(dāng)曲線覆蓋寬范圍的水平和形狀時(shí)，尤其如此，如例3（表7）所示。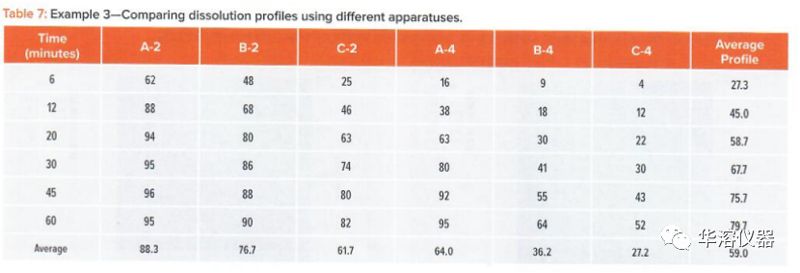

在圖9中，我們看到了曲線從小的曲率（B-4和C-4）到大的曲率（剖面A-4和A-2）。表7和圖9中的數(shù)據(jù)來自一項(xiàng)研究，涉及三種產(chǎn)品，A、B和C，由兩臺(tái)設(shè)備進(jìn)行分析。USP2和USP4。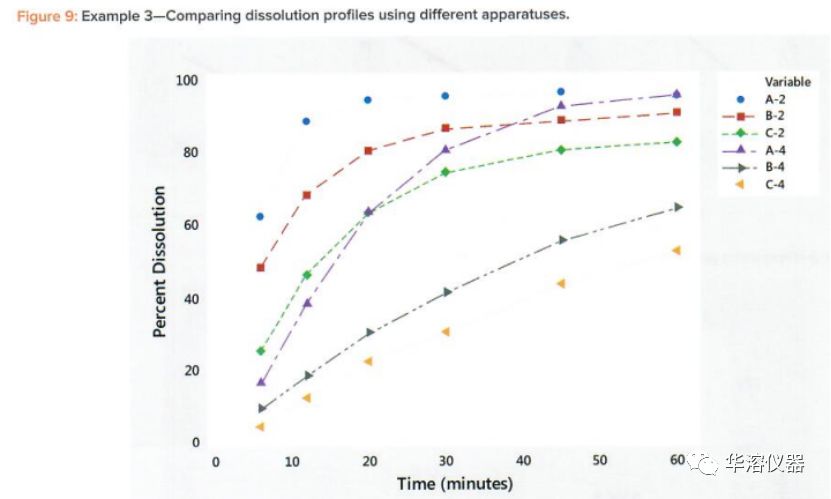

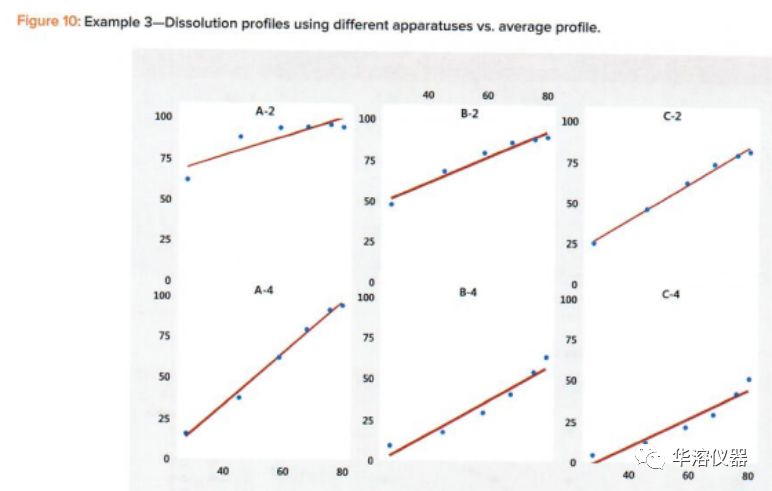
在圖10和表8中，我們看到，除了A-2外，所有的線性擬合都非常好，其中平均曲線相關(guān)性為0.918。所有其他相關(guān)系數(shù)的范圍為0.968至0.998（表8）。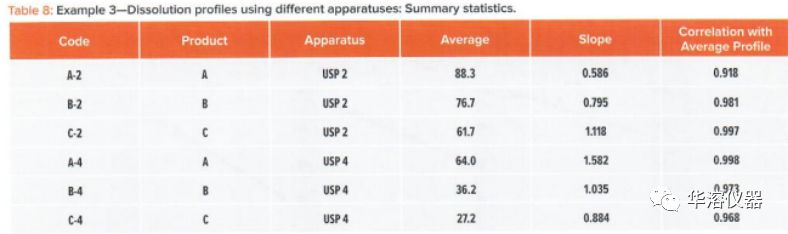
在圖11所示的DP斜率與水平的關(guān)系圖中，我們看到兩個(gè)裝置產(chǎn)生不同的DP。我們看到了水平和斜率之間的關(guān)系，但這兩種儀器導(dǎo)致的關(guān)系不同。圖12顯示了兩個(gè)裝置的DP差異。我們還可以在圖11中看到，產(chǎn)品A（USP4）與所有其他不同。產(chǎn)品A的不同DP在圖11和圖12中都很明顯。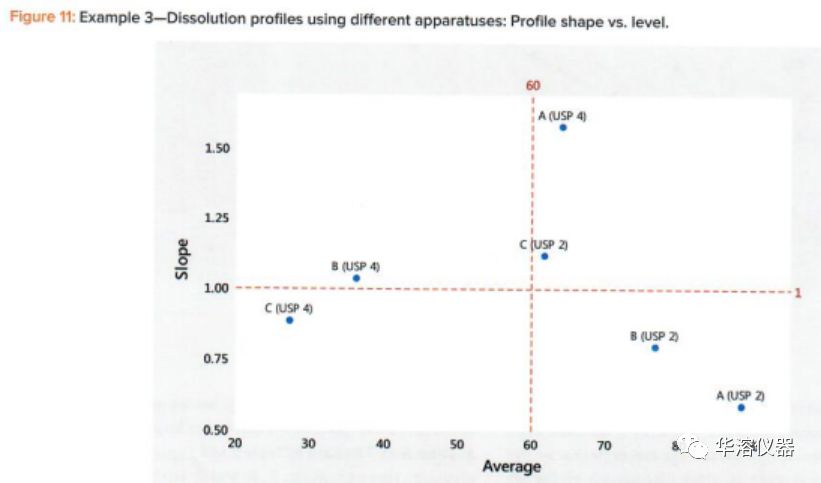
如前面所述，在DP線性化所提出方法的步驟4的討論中，當(dāng)繪制與平均曲線的對(duì)比作為使曲線線性化的方法時(shí)，可以使用Wang和合著者討論的MPCA。
盡管MPCA給出了更好的擬合，但結(jié)論沒有改變。這導(dǎo)致了一個(gè)推測(cè)，這一推測(cè)得到了其他溶出研究分析的支持，即即使在線性擬合不完美的情況下，平均曲線也能捕捉到曲線的大部分差異。無論如何，我們得出的結(jié)論是，一個(gè)好的方法是將平均曲線作為DP建模的首選。如果需要或期望更好的擬合，則應(yīng)使用MPCA方法。
四、總結(jié)：有效的溶出曲線分析策略
DP是藥物的關(guān)鍵特性。本文介紹了一種方法，它克服了以前可用方法的許多限制。該方法提供與DP水平和形狀相關(guān)的統(tǒng)計(jì)信息。這是通過找到使DP線性化來實(shí)現(xiàn)的。平均DP是一種在許多不同情況下都能使用的因子。這種方法在統(tǒng)計(jì)上不如MPCA方法復(fù)雜與先進(jìn)。然而，它非常有效，具有廣泛的實(shí)用性，相關(guān)的計(jì)算更容易執(zhí)行。當(dāng)需要更接近DP的方法時(shí)，建議使用MPCA方法。這兩種方法都將DP簡(jiǎn)化為兩個(gè)統(tǒng)計(jì)數(shù)據(jù)：水平和形狀。然后使用適用于生成DP方法對(duì)這些統(tǒng)計(jì)數(shù)據(jù)進(jìn)行分析，如示例2所示。大多數(shù)統(tǒng)計(jì)軟件包都提供了所需的計(jì)算。統(tǒng)計(jì)分析結(jié)果易于理解，并與實(shí)驗(yàn)的實(shí)際背景相關(guān)。當(dāng)進(jìn)行MPCA的結(jié)果不明確時(shí)，建議使用這兩種方法并比較總體結(jié)論。如果MPCA提供的額外信息很少或沒有，那么人們對(duì)線性化溶出曲線斜率和溶出曲線平均值分析結(jié)果的信心就會(huì)增加。
五、參考文獻(xiàn)
略
如需原文，請(qǐng)聯(lián)系小編（15012941165）